T-test je nástroj umožňující ověřit, zdali dva výběry mají (v rámci stanovené hladiny významnosti) stejnou střední hodnotu, příp. jestli se jejich střední hodnoty liší o předem stanovený rozdíl. Excel nabízí tři varianty t-testu a navíc ještě podobný z-test.
NahoruDvouvýběrový párový t-test na střední hodnotu
Máme dva výběry se spárovanými hodnotami, tedy se stejným počtem hodnot v obou výběrech. Typicky jde o výsledky dvojího testování jedinců též skupiny – např. před provedením experimentu a po něm. Ve výběrech je přitom zachováno pořadí jedinců. Jako konkrétní příklad uveďme zhodnocení zdravotního stavu pacientů před podáním léků a po něm.
Na listu máme připravené dva výběry.
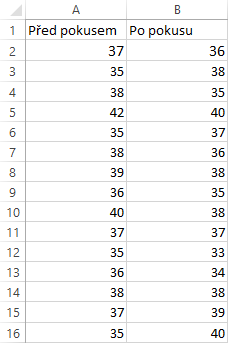
Na kartě Data klikneme na tlačítko Analýza dat a zvolíme nástroj Dvouvýběrový párový t-test na střední hodnotu (pokud na kartě Data toto tlačítko nemáme, tak je potřeba aktivovat doplněk Analytické nástroje – viz první díl seriálu).
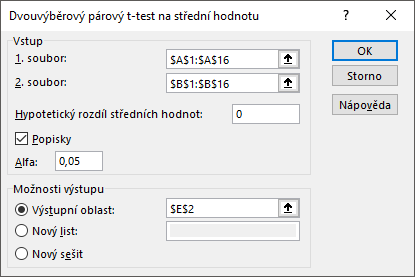
Pomocí polí 1. soubor a 2. soubor označíme výběry. Chceme-li ověřit, zdali mají výběry stejnou střední hodnotu, tak ponecháme pole Hypotetický rozdíl středních hodnot prázdné nebo zde zapíšeme nulu. Na pořadí výběrů v takovém případě nezávisí.
Chceme-li ověřit, že se střední hodnoty liší o předem stanovanou hodnotu, tak ji do tohoto pole zapíšeme. Rozdíl je potřeba zadat kladný a předpokládá se, že střední hodnota prvního výběru je větší než střední hodnota druhého výběru.
Jsou-li v záhlaví výběrů zapsány jejich názvy, tak zaškrtneme volbu Popisky. Výchozí hodnota hladiny významnosti Alfa je 0,05. V případě potřeby ji změníme. V části Možnosti výstupu pak určíme, kde se má vytvořit výstupní tabulka.
Výstupní tabulka obsahuje i základní statistické charakteristiky výběru – aritmetický průměr (Stř. hodnota), rozptyl a počet hodnot (Pozorování). Klíčové pro interpretaci výsledků t-testu jsou ale hodnoty t Stat a t krit (2).
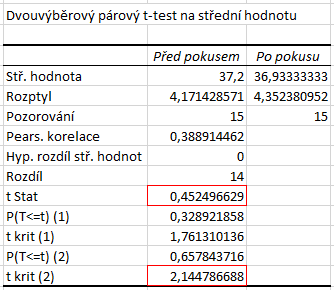
Znaménko hodnoty t Stat je závislé na pořadí výběrů. Při porovnávání s kritickou hodnotou se proto bere absolutní hodnota t Stat.
Nulová hypotéza zní: výběry mají shodné střední hodnoty (resp. obecněji rozdíl střední hodnoty prvního výběru a střední hodnoty druhého výběru je roven hodnotě zadané v poli Hypotetický rozdíl středních hodnot).
Alternativní hypotéza zní: výběry mají rozdílné střední hodnoty.
Je-li |t Stat|<t krit (2), tak platí nulová hypotéza, tj. střední hodnoty jsou shodné.
Je-li |t Stat|>t krit (2), tak platí alternativní hypotéza, tj. střední hodnoty jsou rozdílné.
O výběrech testovaných v našem příkladu tedy…